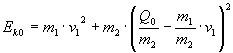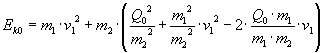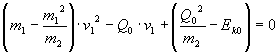Trivial:
![]()
They’re touching iff ![]()
Bouncing balls, geometry and physics
©2000 Marco Brandizi
The core of the question is calculating the new speed vectors, after having stated two balls are bouncing together.
The key is working along the line joining the centers of the balls. I’ll consider here the case of the same masses (set to unitary value).
The stuff is arranged with following steps.
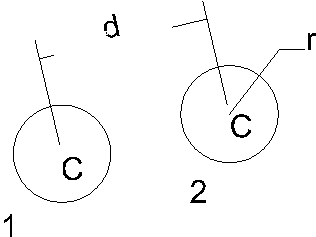
1) Are they touching?
|
Trivial:
They’re touching iff |
|
2) Find ![]() direction
direction
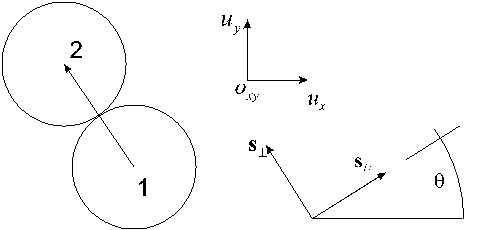
Ok, they’re touching. We’ll need the direction of ![]() vector, the line joining the balls centers (with
vector, the line joining the balls centers (with ![]() as positive direction). So, let’s find
as positive direction). So, let’s find ![]() (i.e.: cosine and sine).
(i.e.: cosine and sine).
![]()
![]()
![]()
![]()
![]()
3) Find the speed components along the centers line
Now we have the angle, we can find the speed components on the ![]() system.
system.
For a single ball:
![]()
Using the rotation equations:
![]()
![]()
![]()
4) Apply physics
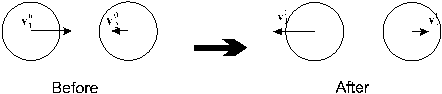
Now it’s easy to apply the physics of the system to the calculated components:
The // components don’t vary. For the ![]() components:
components:
![]()
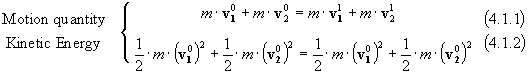
Setting:
![]()
![]()
![]()
We have:
![]() from (4.1.1)
from (4.1.1)
![]() from (4.1.2)
from (4.1.2)
And also:
![]()
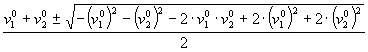
![]()
The first solution refers to the case of balls not crashing, the second, the meaning one, says the speeds are exchanged.
4.1) Signs checking
After having stated the balls are touching we need also a check about the signs of ![]() and
and ![]() :
:
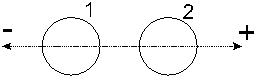
++ They’re really crashing together (if ![]() )
)
+- Crashing
-- Crashing ( ![]() )
)
-+ Moving away
(In fact, in an animation program we also have to track the crash event in order to avoid its continuos firing when balls are near enough)
5) Back to ordinary Cartesian space
When you have new ![]() speed components, and therefore new speed vectors, expressed in terms of
speed components, and therefore new speed vectors, expressed in terms of ![]() and // components, you have to back to the Oxy coordinates system, with the rotation:
and // components, you have to back to the Oxy coordinates system, with the rotation:
![]()
Resume:
Appendix: A brief view about the case of different masses
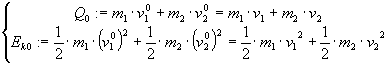
![]()
![]()